This note is to remind myself about some of the basic concepts of linear regression.

Bibliography

[1] James, Witten, Hastie, Tibshirani - Introduction to Statistical Learning

Setup¶

In [1]:

import numpy as np
import scipy.stats
import pandas as pd
import matplotlib.pylab as plt

In [2]:

%matplotlib inline

In [3]:

(blue, orange, red, green, purple, brown, pink, yellow, lightred, lightblue,
lightorange, lightgreen, lightpurple) = \
('#377eb8', '#ff7f00', '#e41a1c', '#4daf4a', '#984ea3', '#a65628', '#f781bf',
'#d2d215', '#fb9a99', '#a6cee3', '#fdbf6f', '#b2df8a', '#cab2d6')

Creating some (noisy) toy data¶

In [4]:

def create_data(b0, b1, noise_sd, n=100):
    """Return a dataframe with `n` rows and columns 'X' and 'Y'
    The dataframe will contain random data points that follow
    ``Y = b1 * X + b0 + eps`` where the error `eps` is drawn from
    a normal distribution with standard deviation `noise_sd`
    """
    x = np.sort(10 * np.random.rand(n))
    y = b1 * x + b0
    noise = scipy.stats.norm(scale=noise_sd)
    y += noise.rvs(len(x))
    return pd.DataFrame({'X': x, 'Y': y})

In [5]:

b0_true = 0.3
b1_true = 1.2
noise_sd = 2.0  # σ in the standard distribution

data = create_data(b0_true, b1_true, noise_sd)

def plot_data(data, *lines, show=True, **kwargs):
    fig, ax = plt.subplots(**kwargs)
    data.plot.scatter('X', 'Y', ax=ax)
    for (b0, b1, label, color) in lines:
        ax.plot(
            np.linspace(0, 10, 5),
            b0 + np.linspace(0, 10, 5) * b1,
            color=color, label=label)
    ax.legend()
    if show:
        plt.show(fig)
    else:
        return fig, ax
    
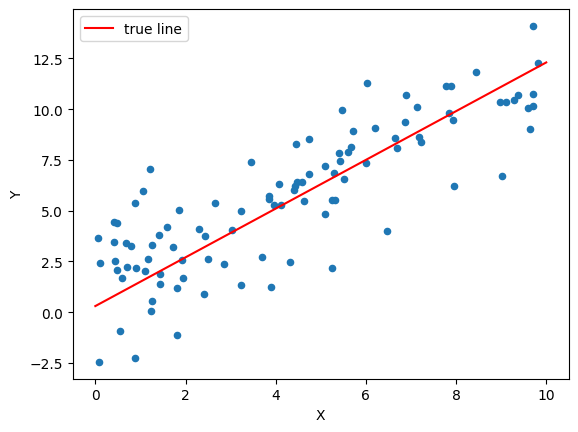
plot_data(data, (b0_true, b1_true, 'true line', 'red'))

Linear Regression with statsmodels¶

In [6]:

import statsmodels.api as sm

In [7]:

mod = sm.OLS(data['Y'], sm.add_constant(data['X']))

In [8]:

res = mod.fit()
res.summary()

Out[8]:

OLS Regression Results
Dep. Variable:	Y	R-squared:	0.699
Model:	OLS	Adj. R-squared:	0.696
Method:	Least Squares	F-statistic:	228.0
Date:	Sun, 22 Jan 2023	Prob (F-statistic):	2.55e-27
Time:	12:08:04	Log-Likelihood:	-207.72
No. Observations:	100	AIC:	419.4
Df Residuals:	98	BIC:	424.7
Df Model:	1
Covariance Type:	nonrobust

	coef	std err	t	P>\|t\|	[0.025	0.975]
const	1.3407	0.346	3.876	0.000	0.654	2.027
X	1.0144	0.067	15.098	0.000	0.881	1.148

Omnibus:	2.898	Durbin-Watson:	2.206
Prob(Omnibus):	0.235	Jarque-Bera (JB):	2.676
Skew:	-0.400	Prob(JB):	0.262
Kurtosis:	2.960	Cond. No.	9.36

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

In [9]:

res.params

Out[9]:

const    1.340737
X        1.014445
dtype: float64

Manual Linear Regression¶

In [10]:

def linear_regression(data):
    """Estimated b0_hat, b1_hat for the given data.

    See [1] Eq. (3.4)
    """
    xbar = data['X'].mean()
    ybar = data['Y'].mean()
    delta_x = data['X'] - xbar
    delta_y = data['Y'] - ybar
    b1_hat = np.dot(delta_x, delta_y) / np.dot(delta_x, delta_x)
    b0_hat = ybar - b1_hat * xbar
    return b0_hat, b1_hat

In [11]:

b0_hat, b1_hat = linear_regression(data)

In [12]:

b0_hat, b1_hat

Out[12]:

(1.3407370728448775, 1.0144446957055053)

In [13]:

b0_true, b1_true

Out[13]:

(0.3, 1.2)

In [14]:

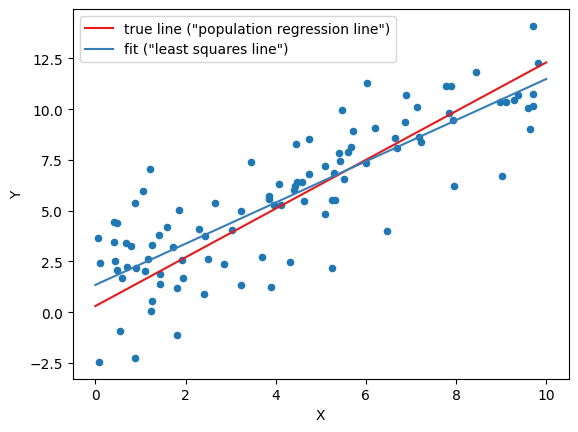
plot_data(
    data,
    (b0_true, b1_true, 'true line ("population regression line")', red),
    (b0_hat, b1_hat, 'fit ("least squares line")', blue)
)

Goodness of Fit¶

Standard Error¶

The Standard Error describes how close an estimated quantity is expected to be to the actual quantity.

It is the standard deviation of the "sampling distribution" of a statistical quantity: If you take a large number of independent samples, each of size $n$, and calculate the statistical quantity for each sample individually, then the standard errror is the standard deviation of the distribution of those results. It is always $\sigma/\sqrt{n}$, where $\sigma$ is the (possibly unknown) standard deviation of the original distribution. Standard errors go to zero as sample sizes go to infinity; standard deviations do not.

In [15]:

def residuals(data, b0, b1):
    """Array of residuals from the perfect linear relation ``Y=b1*X+b0``"""
    Y_hat = b1 * data['X'] + b0
    return data['Y'] - Y_hat

In [16]:

def RSS(data, b0, b1):
    """Residual Sum of Squares
    
    How much the Y values vary around the predicted Y values 
    """
    return (residuals(data, b0, b1)**2).sum()

In [17]:

def TSS(data):
    """Total Sum of Squares
   
    How much the Y values vary around the mean Y value
    """
    return ((data['Y'] - data['Y'].mean())**2).sum()

In [18]:

def RSE(data, b0, b1):
    """Residual standard error
    
    This is an estimate for the standard deviation σ of the true
    distribution (noise_sd). The y-values in the sample deviate from the 
    from the true regression line by about RSE units on average.
    """
    return np.sqrt(RSS(data, b0, b1) / (len(data)-2))

In [19]:

RSS(data, b0_hat, b1_hat)

Out[19]:

373.07675962480016

In [20]:

RSE(data, b0_hat, b1_hat)

Out[20]:

1.9511293423187364

In [21]:

noise_sd

Out[21]:

2.0

In [22]:

def linear_regression_SE(data, sig):
    """Calculate the standard error for the estimate of b0, b1 in a
    linear regression for the given data, assuming a standard deviation of
    `sig` for the distribution of noise on Y. As `sig` is generally not known,
    it should be estimated by the RSE.
    
    Note that the standard error is a property of the sampling only:
    The `Y`-values do not enter!
    
    See [1] Eq. (3.8)
    """
    n = len(data)
    xbar = data['X'].mean()
    delta_x = data['X'] - xbar
    denom = np.dot(delta_x, delta_x)
    se_b0_sq = sig**2 * (1.0 / n + xbar**2/denom)
    se_b1_sq = sig**2 / denom
    return np.sqrt(se_b0_sq), np.sqrt(se_b1_sq)

In [23]:

linear_regression_SE(data, RSE(data, b0_hat, b1_hat))

Out[23]:

(0.34590880729195916, 0.06718913728836097)

The 95% confidence intervals is $\pm$ two standard errors (probability that the true value is in the range of the confidence interval)

Confidence Interval plot¶

See https://stats.stackexchange.com/questions/85560/shape-of-confidence-interval-for-predicted-values-in-linear-regression/85565#85565m for the full explanation and derivation.

In [24]:

def regline_SE(data, sig, xgrid):
    """The standard error of the full regression line, assuming 
    a standard deviation of `sig` for the distribution of noise on Y. As
    `sig` is generally not known, it should be estimated by the RSE.
    """
    n = len(data)
    return sig * np.sqrt(
        (1.0 / n) + (
            (xgrid - data['X'].mean())**2 /
            ((data['X'] - data['X'].mean())**2).sum()))

The 95% confidence band can be calculated as:

In [25]:

def regline_confidence_bands(data, b0_hat, b1_hat, xgrid, confidence=0.95):
    """Return two lines (arrays of y-values), the lower and upper boundary
    of the confidence band"""
    Y_hat = b0_hat + b1_hat * xgrid  # the fitted line, on the given xgrid
    n = len(data)
    sig = RSE(data, b0_hat, b1_hat)
    se = regline_SE(data, sig, xgrid)
    t_minus, t_plus = scipy.stats.t(df=n-2).interval(confidence)
    return Y_hat + t_minus * se, Y_hat + t_plus * se

In [26]:

fig, ax = plot_data(
    data,
    (b0_true, b1_true, 'true line ("population regression line")', red),
    (b0_hat, b1_hat, 'fit ("least squares line")', blue),
    show=False, figsize=(10, 6)
)
xgrid = np.linspace(0, 10, 100)
lm, lp = regline_confidence_bands(data, b0_hat, b1_hat, xgrid)
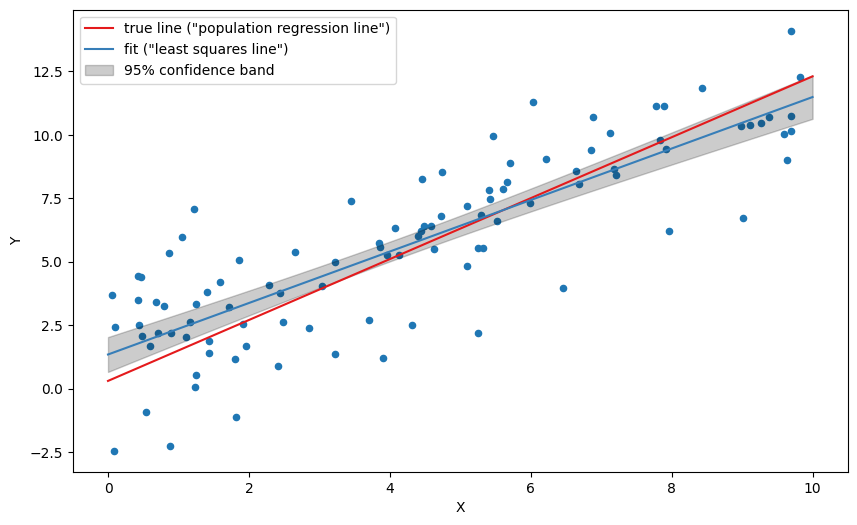
ax.fill_between(
    xgrid, lm, lp,
    color='black', alpha=0.2, label='95% confidence band')
ax.legend()
plt.show(fig)

The confidence band should be interpreted as follows: There is a 95% probability that a fit based on any given sampling of the same distribution will land in the interval.

Testing the null hypothesis¶

The null-hypthesis is that Y and X have no reltionship, i.e. b1 = 0. The $t$-value is the b1 in units of the standard error:

In [27]:

t = b1_hat / linear_regression_SE(data, RSE(data, b0_hat, b1_hat))[1]
t

Out[27]:

15.09834381935479

The $t$-value follows a student distribution, and we can calculate a p-value (probability that $t$ has the given value, instead of 0)

In [28]:

2 * scipy.stats.t(df=len(data)-2).sf(t)  # = 1 - (cdf(t) - cdf(-t))

Out[28]:

2.5471330315828787e-27

The $R^2$ statistic¶

In [29]:

def R_sq(data, b0, b1):
    """R^2 in [0, 1] measures how well the variation in Y around the mean
    matches the variation in Y around the predicted value.
    
    That is, how much of the variability can be explained by the sampling"""
    return 1 - RSS(data, b0, b1) / TSS(data)

In [30]:

R_sq(data, b0_hat, b1_hat)

Out[30]:

0.6993496006172107

A value close to 1 means that the linear fit is very good

Normality of the residuals¶

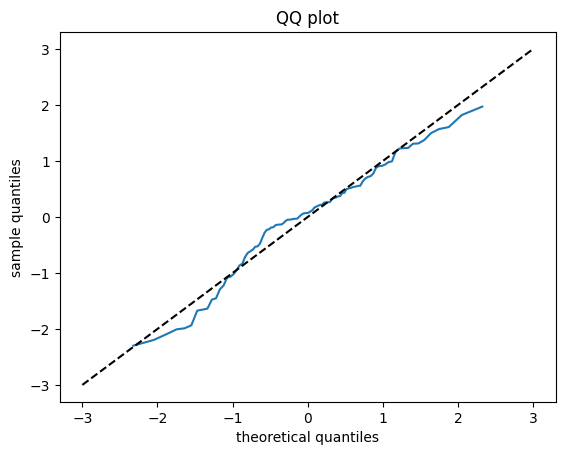
A graphical way to check that the residuals are normal-distributed is to plot the quantiles of the residules against the quantiles of a normal distribution, see https://stats.stackexchange.com/questions/321061/probability-that-residuals-are-normal/321071#321071

In [31]:

fig, ax = plt.subplots()
ax.plot(
    scipy.stats.norm().ppf(np.linspace(0, 1, len(data))),
    residuals(data, b0_hat, b1_hat).sort_values() / RSE(data, b0_hat, b1_hat))
ax.set_title('QQ plot')
ax.plot(
    np.linspace(-3, 3, 10), np.linspace(-3, 3, 10), color='black',
    ls='dashed')
ax.set_xlabel('theoretical quantiles')
ax.set_ylabel('sample quantiles')
plt.show(fig)

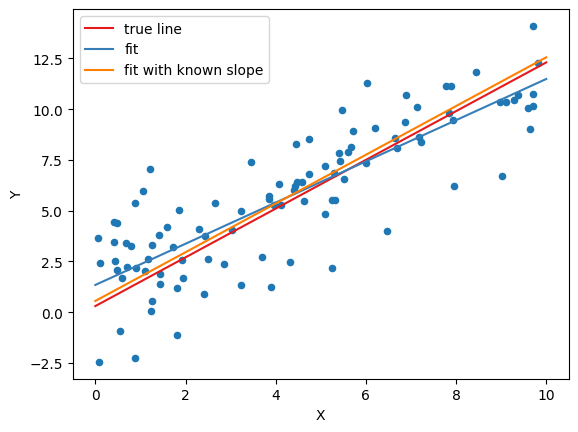
Fit with known slope¶

In [32]:

b0_known_slope = np.mean(data['Y'] - b1_true*data['X'])

In [33]:

b0_known_slope

Out[33]:

0.5519198289545456

In [34]:

b0_true

Out[34]:

0.3

In [35]:

plot_data(
    data,
    (b0_true, b1_true, 'true line', red),
    (b0_hat, b1_hat, 'fit', blue),
    (b0_known_slope, b1_true, 'fit with known slope', orange),
    show=True,
)